

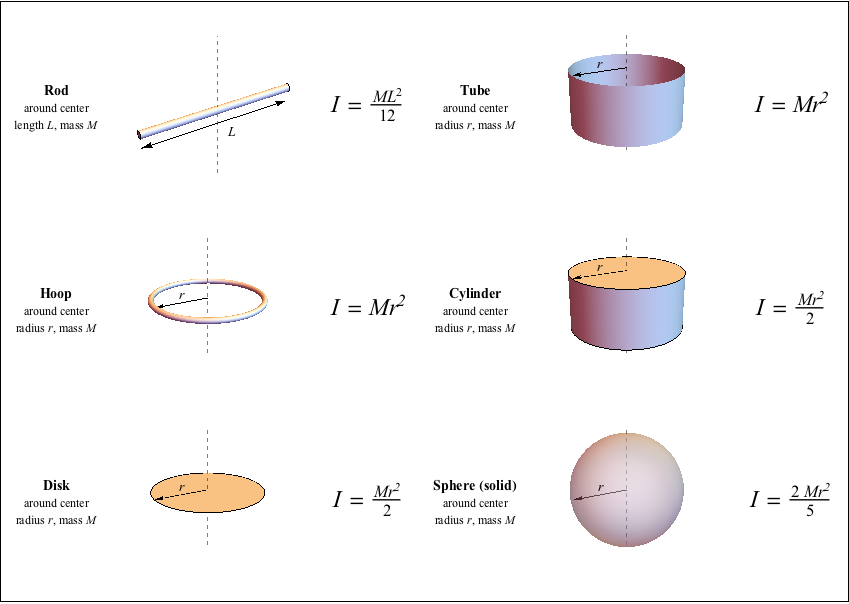

Therefore, it can be seen from the former equation, that when a certain bending moment M is applied to a beam cross-section, the developed curvature is reversely proportional to the moment of inertia I. Where Ixy is the product of inertia, relative to centroidal axes x,y (=0 for the I/H section, due to symmetry), and Ixy' is the product of inertia, relative to axes that are parallel to centroidal x,y ones, having offsets from them d_. This equation is equivalent to I D 4 / 64 when we express it taking the diameter (D) of the circle. The integration limits depend on how you set up your dm. Therefore, if your result doesn’t have those units, then you know you have made a mistake. Things to keep in mind The units of the moment of inertia are kgm 2. Where I' is the moment of inertia in respect to an arbitrary axis, I the moment of inertia in respect to a centroidal axis, parallel to the first one, d the distance between the two parallel axes and A the area of the shape, equal to 2b t_f + (h-2t_f)t_w, in the case of a I/H section with equal flanges.įor the product of inertia Ixy, the parallel axes theorem takes a similar form: Moment Of Inertia Of A Circle Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression I R 4 / 4 Here, R is the radius and the axis is passing through the centre. Because m/V and V R2 L, we get for the moment of inertia: Which is the answer. Using the density we get the following for the whole triangle: I I 1 + I 2 ( h w 1 3 4 + h 3 w 1 12) + ( h w 2 3 4 + h 3 w 2 12) Then of course we can use the parallel axis theorem. The so-called Parallel Axes Theorem is given by the following equation: The moment of inertia for the whole triangle rotating about p3 is the sum of the moments of inertia of the two right triangle halves rotating about p3. The formula and derivation can be found in this thread. For the polar moment of inertia, which is what you would use to calculate the force for a bolt group where a moment is about the centroid of the bolt group, is Ix + Iy. The area moment is defined over the centroid, which is the centre of the x and y axes. The moment of inertia of the bolts themselves about their individual centroids is ignored as being inconsequential.
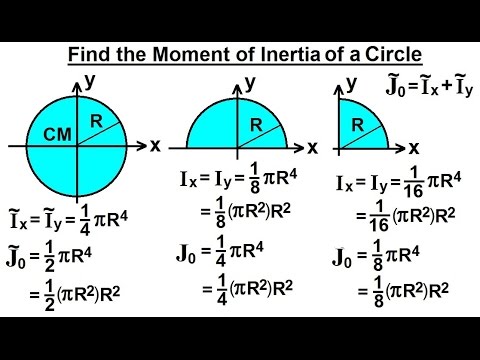
Circle where r is the radius of the circle for which area moment of inertia is to be evaluated. To calculate the area moment of inertia through calculus equation 1 would be used for a general form.The moment of inertia of any shape, in respect to an arbitrary, non centroidal axis, can be found if its moment of inertia in respect to a centroidal axis, parallel to the first one, is known. Area moment of inertia is defined w.r.t the x and y axes, respectively. Note that when using the parallel axis theorem, area is always positive, and the MOI of the hole I 2 is subtracted from I 1 to get the MOI of the combined shape. However, there are certain cases where the area moment of inertia will have to be calculated either through calculus or by manipulating the equations found in this table.Īrea Moment if Inertia Calculator Width (b): Demonstrates calculation of the moment of inertia of a composite shape about the x axis using the parallel axis theorem. For basic shapes there are tables that contain area moment of inertia equations which can be viewed below. In the same manner, the transfer formula for polar moment of inertia and the radii of gyration are respectively. It is determined from the cross-sectional area of the beam and the central axis for the direction of interest. Knowing the area moment of inertia is a critical part of being able to calculate stress on a beam.


 0 kommentar(er)
0 kommentar(er)
